# MM
# markov model:
马尔可夫模型,指的是在给定当前知识的情况下,过去对于预测未来是无关的,诶个状态的转移,只依赖之前的 n 个状态,被称为是一个 n 阶模型。
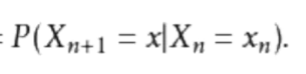
# 转移矩阵:
指的是从一个状态转移到另一个状态的概率,整体上为一个 n*n 的矩阵
# HMM
用来描述 含有隐含未知参数的马尔可夫过程。对于投色子来讲,假如有三种色子,分别包含 6 8 10 个面,那么每个色子表现出 1 的概率是不同的,同时,我们还知道色子丢出来的结果到底是几,那么我们就可以用这个结果去反推出对应的值是由哪个色子投出来的。
# HIDDEN STATE:
隐藏状态集合
# Observations state:
观测状态集合
# Start Probability:
隐藏状态初始化的概率值
# Hidden Transition_Probability:
隐藏状态概率转移矩阵
# Hidden to Observations Probability:
隐藏状态到观测状态概率集合
# Viterb 算法
本质上是动态规划,假设初始状态有 n 种,观测序列的长度为 m,那么总共的路径数就为 m 的 n 次方,要想从中找到最优路径往往是不显示的,但是,对于一段长度为 x 路径来说,要是该路径是最优的,那么其长度为 x-1 的子路径也一定是最优的,那么问题就变为了,根据每一条路径,在其基础上,找到其距下个节点的最优路径即可,这样问题就缩小为了 m*n 个,极大降低了复杂度。
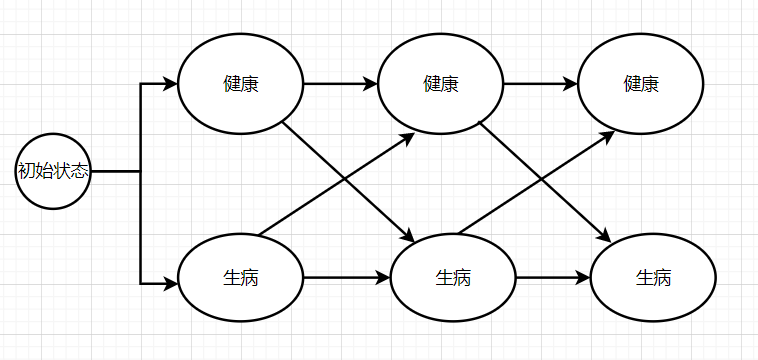
# DEMO (以一个看病为例)
首先定义了隐藏状态:健康、生病
观测序列:正常,冷,发烧 (这里指代我们看到的情况)
初始概率:健康:0.6 生病:0.4
隐藏状态概率转移矩阵:健康到健康 0.7 健康到生病 0.3 生病到健康 0.4 生病到生病 0.6’
隐藏状态到观测状态概率集合:
"Healthy": {"normal": 0.5, "cold": 0.4, "dizzy": 0.1}, | |
"Fever": {"normal": 0.1, "cold": 0.3, "dizzy": 0.6}, |
我们要根据观测序列推断出其真实情况,在这里每一条路径都是由上一时刻的状态 X 隐藏状态转移概率矩阵 X 隐藏状态到观测状态概率集合 (这里要针对每一个隐藏状态,因为需要对这个隐藏状态进行解码).
python 实现:
Hidden_states = ("Healthy", "Fever") # 隐状态集合 | |
Observations_states = ("normal", "cold", "dizzy") # 观测状态集合 | |
Start_probability = { | |
"Healthy": 0.6, | |
"Fever": 0.4, | |
} # 表示病人第一次到访时医生认为其所处的 HMM 状态,他唯一知道的是病人倾向于是健康的(可以理解为这是基于一个对大众身体信息的了解得出的初始状态) | |
2*2 | |
Hidden_transition_probability = { # 隐马尔可夫链中身体状态的状态转移概率,我们能够看到,当天健康的人,第二天有 30% 的概率会发烧 | |
"Healthy": {"Healthy": 0.7, "Fever": 0.3}, | |
"Fever": {"Healthy": 0.4, "Fever": 0.6}, | |
} | |
3 | |
Hidden_observations_probability = ( | |
{ # 原来叫 emission_probability。这里表示病人每天的感觉的可能性。即,如果他是一个健康人,有 50% 的可能会感觉正常,40% 觉得冷,10% 觉得头晕 | |
"Healthy": {"normal": 0.5, "cold": 0.4, "dizzy": 0.1}, | |
"Fever": {"normal": 0.1, "cold": 0.3, "dizzy": 0.6}, | |
} | |
) | |
def viterbi(obs, states, start_p, trans_p, h2o_p): # Viterbi 算法 | |
V = [{}] | |
path = {} | |
# Initialize base cases (t == 0) | |
# | |
for y in states: | |
V[0][y] = start_p[y] * h2o_p[y][obs[0]] | |
# 初始状态,由 start 的概率,对应乘上发射概率,即由隐状态到观测状态的可能性 | |
path[y] = [y] # 记录下相应的路径 | |
# Run Viterbi for t > 0,每天都要更新计算一遍 | |
for t in range(1,len(obs)): | |
V.append({}) | |
newpath = {} | |
for y in states: | |
# 对于每个状态,计算其由前一天的各个状态,到达今天的 y 的概率大小,与 y0 自身相比较,取最大值 | |
# 前一天到达今天的每个状态对应的路径大小都计算了,取最大值。作为 V [t][y] 的值,并更新路径 | |
# print('V[t-1]:',V[t-1],'trans_p:',trans_p,'h2o_p[y]:',h2o_p[y],[V[t-1][y0] * trans_p[y0][y] * h2o_p[y][obs[t]] for y0 in states]) | |
(prob, state) = max([(V[t-1][y0] * trans_p[y0][y] * h2o_p[y][obs[t]], y0) for y0 in states]) | |
print(V[t],y) | |
V[t][y] = prob | |
newpath[y] = path[state] + [y] | |
# Don't need to remember the old paths | |
path = newpath | |
# print(path) | |
# print_dptable(V) | |
# 最后一天 | |
(prob, state) = max([(V[len(obs) - 1][y], y) for y in states]) | |
return (prob, path[state]) | |
def example(): | |
return viterbi(Observations_states, | |
Hidden_states, | |
Start_probability, | |
Hidden_transition_probability, | |
Hidden_observations_probability) | |
print(example()) |
# 实际案例
已知:
- 观测序列 (指历年主题比重)
- 状态转移矩阵:共现词矩阵 (需要进行一个归一化)
目的:使用 Baum-Welch 算法,根据 12-21 年的比重,预测 22-25 年的比重
